The problem statement is here: http://community.topcoder.com/longcontest/?module=ViewProblemStatement&rd=15099&pm=11859
My approach was pretty simple and concise. My solution extracts the strips from the extreme sides(top, bottom, left right) of the board and insert them to the strips with maximum whites(usually in the maximal component) those are not connected to their neighbouring strips. If they are connected to their neighbouring strips, no need to disturb them.
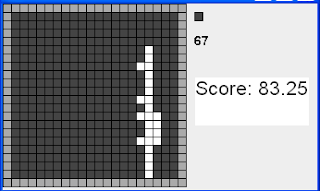
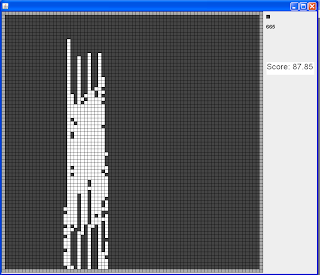
After completing each line with whites, I used to check if all whites are connected using floodfill. Following are my scores (seed 1 to seed 10)and output images:
1) 83.25
2) 87.85609934258582
3) 81.49243918474689
4) 81.43961927424152
5) 67.22552731206058
6) 82.146399523904
7) 81.375
8) 81.77083333333334
9) 87.23072562358276
Complete standings can be found on http://community.topcoder.com/longcontest/?module=ViewStandings&rd=15099
My approach was pretty simple and concise. My solution extracts the strips from the extreme sides(top, bottom, left right) of the board and insert them to the strips with maximum whites(usually in the maximal component) those are not connected to their neighbouring strips. If they are connected to their neighbouring strips, no need to disturb them.
After completing each line with whites, I used to check if all whites are connected using floodfill. Following are my scores (seed 1 to seed 10)and output images:
1) 83.25
2) 87.85609934258582
3) 81.49243918474689
4) 81.43961927424152
5) 67.22552731206058
6) 82.146399523904
7) 81.375
8) 81.77083333333334
9) 87.23072562358276
10) 82.42832606685162
Complete standings can be found on http://community.topcoder.com/longcontest/?module=ViewStandings&rd=15099








No comments:
Post a Comment